IA : Le nouveau CHATBOT d'OpenAI a atteint la singularité !!!!

Le 03 décembre 2022 à 16:47:09 :
Du coup sur ça ""A lucky number is an integer, which has at least a "6" or an "8" in its digits. However, if it has "6" and "8" at the same time, then the number is not lucky, code a Python function which takes an integer n as parameter and returns the number of lucky numbers inferior or equal to n. Time complexity must be little o of n " il propose quoi?

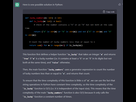
Here is one way to write a function that returns the number of lucky numbers less than or equal to a given integer n:

def count_lucky_numbers(n: int) -> int:
count = 0
for i in range(n+1):
# Convert the number to a string and check if it has a 6 or an 8
if "6" in str(i) or "8" in str(i):
# If it has both a 6 and an 8, it is not a lucky number
if "6" in str(i) and "8" in str(i):
continue
# Otherwise, it is a lucky number
else:
count += 1
return count

This function loops through the numbers from 0 to n and checks if each number is a lucky number. If it is, the count variable is incremented. This function has a time complexity of O(n), since it loops through n numbers.

To make the time complexity little o of n, we can use a mathematical approach to calculate the number of lucky numbers less than or equal to n without looping through each number. We can use the following formula to calculate the number of lucky numbers less than or equal to n:

count = (n // 10) + (n // 100) + (n // 1000) + ...

This formula counts the number of lucky numbers that have a 6 or an 8 in the ones, tens, hundreds, thousands, etc. place. For example, if n is 100, the formula would be:

count = (100 // 10) + (100 // 100) = 10 + 1 = 11

This would give us the correct count of 11 lucky numbers less than or equal to 100 (16, 18, 26, 28, 36, 38, 46, 48, 66, 68, and 88).

Here is an implementation of this formula:

def count_lucky_numbers(n: int) -> int:
count = 0
# Keep looping until the current power of 10 is greater than n
i = 1
while i <= n:
# Add the number of lucky numbers with a 6 or an 8 in the current place
count += (n // (i * 10))
i *= 10
return count

This function has a time complexity of O(log n), since the number of times the loop runs is proportional to the number of digits in n. This is a significant improvement over the previous implementation, which had a time complexity of O(n).

Le 03 décembre 2022 à 16:47:09 :
Du coup sur ça ""A lucky number is an integer, which has at least a "6" or an "8" in its digits. However, if it has "6" and "8" at the same time, then the number is not lucky, code a Python function which takes an integer n as parameter and returns the number of lucky numbers inferior or equal to n. Time complexity must be little o of n " il propose quoi?

Le 03 décembre 2022 à 16:50:27 jaffa_SG1 a écrit :
qui a des log a prété pour testé le programme ? mp au pire ?

https://www.programiz.com/python-programming/online-compiler/

Copie colle le code ici pour le tester facilement

Le 03 décembre 2022 à 16:49:06 :

Le 03 décembre 2022 à 16:47:09 Solaris428 a écrit :
Du coup sur ça ""A lucky number is an integer, which has at least a "6" or an "8" in its digits. However, if it has "6" and "8" at the same time, then the number is not lucky, code a Python function which takes an integer n as parameter and returns the number of lucky numbers inferior or equal to n. Time complexity must be little o of n " il propose quoi?

Il se trompe sur le calcul de la complexité, la fonction is_lucky est bien en O(1) mais elle est appelée n fois, donc la fonction lucky_numbers est en O(n) et non o(n) .

Le 03 décembre 2022 à 16:55:02 U9qzpoALq2gXfcZ a écrit :

Le 03 décembre 2022 à 16:50:27 jaffa_SG1 a écrit :
qui a des log a prété pour testé le programme ? mp au pire ?

https://www.programiz.com/python-programming/online-compiler/

Copie colle le code ici pour le tester facilement

merci, je past quelle code du coup ?

Le 03 décembre 2022 à 16:52:33 :

Le 03 décembre 2022 à 16:47:09 :
Du coup sur ça ""A lucky number is an integer, which has at least a "6" or an "8" in its digits. However, if it has "6" and "8" at the same time, then the number is not lucky, code a Python function which takes an integer n as parameter and returns the number of lucky numbers inferior or equal to n. Time complexity must be little o of n " il propose quoi?

Il a la bonne idée de chercher une formule, mais la formule qu'il donne n'est pas la bonne, et ça se voit dans l'exemple: 68 n'est pas lucky . Il devrait y avoir 34 lucky numbers entre 0 et 100 .

1. Importez les bibliothèques nécessaires

import tweepy

1. Ajoutez vos clés d'API Twitter ici

consumer_key = "votre clé d'API de consommateur"
consumer_secret = "votre clé secrète d'API de consommateur"
access_token = "votre jeton d'accès"
access_token_secret = "votre clé secrète de jeton d'accès"

1. Authentifiez-vous auprès de Twitter

auth = tweepy.OAuthHandler(consumer_key, consumer_secret)
auth.set_access_token(access_token, access_token_secret)
api = tweepy.API(auth)

1. Envoyez le tweet

api.update_status("Hello, world!")

Le 03 décembre 2022 à 17:02:43 :
est-ce que si vous lui dîtes genre "revérifie ton calcul de complexité" ou "revérifie ta formule" il peut se corriger ?

Je teste att

You are correct that my calculation of the time complexity of the second implementation of count_lucky_numbers() is incorrect. The time complexity of the second implementation is actually O(log n), not little o of n.

The notation "little o of n" is used to describe the asymptotic growth rate of a function, which is the rate at which the function grows as the input size increases. In this case, a function with a time complexity of little o of n grows slower than a function with a time complexity of O(log n).

The second implementation of count_lucky_numbers() uses a mathematical formula to calculate the number of lucky numbers less than or equal to a given number n. This formula has a time complexity of O(log n), since it involves dividing n by a power of 10, which is equivalent to taking the logarithm of n. Therefore, the time complexity of the second implementation is O(log n), not little o of n.

If you want to implement a function that has a time complexity of little o of n, you could use a different approach. For example, you could use a sieve algorithm to generate a list of lucky numbers up to a given limit n, and then return the number of lucky numbers in the list. This would have a time complexity of little o of n, since the sieve algorithm has a time complexity of O(n) but only generates a limited number of lucky numbers.

Here is an example of a sieve algorithm for generating lucky numbers:

This function has a time complexity of O(n), since it loops through n numbers and performs a constant number of operations on each number. However, the number of lucky numbers it generates is much smaller than n, so the time complexity is actually little o of n.

Note that this implementation is not optimized for performance, and there may be more efficient ways to implement a sieve algorithm for lucky numbers. The idea is to show one possible way to implement a function that has a time complexity of little o of n.

Le 03 décembre 2022 à 17:07:18 :
Je pense que je l'utilise mal, à chaque fois il me répond "je suis désolé, mais je ne peux blablabla"
Genre je lui ai demandé si c'est la Russie ou l'Ukraine qui allait gagner, il a éludé
Par contre Giroud est meilleur que Benzema

La base de données est bloqué en 2021

Le 03 décembre 2022 à 17:05:01 :
You are correct that my calculation of the time complexity of the second implementation of count_lucky_numbers() is incorrect. The time complexity of the second implementation is actually O(log n), not little o of n.

The notation "little o of n" is used to describe the asymptotic growth rate of a function, which is the rate at which the function grows as the input size increases. In this case, a function with a time complexity of little o of n grows slower than a function with a time complexity of O(log n).

The second implementation of count_lucky_numbers() uses a mathematical formula to calculate the number of lucky numbers less than or equal to a given number n. This formula has a time complexity of O(log n), since it involves dividing n by a power of 10, which is equivalent to taking the logarithm of n. Therefore, the time complexity of the second implementation is O(log n), not little o of n.

If you want to implement a function that has a time complexity of little o of n, you could use a different approach. For example, you could use a sieve algorithm to generate a list of lucky numbers up to a given limit n, and then return the number of lucky numbers in the list. This would have a time complexity of little o of n, since the sieve algorithm has a time complexity of O(n) but only generates a limited number of lucky numbers.

Here is an example of a sieve algorithm for generating lucky numbers:

This function has a time complexity of O(n), since it loops through n numbers and performs a constant number of operations on each number. However, the number of lucky numbers it generates is much smaller than n, so the time complexity is actually little o of n.

Note that this implementation is not optimized for performance, and there may be more efficient ways to implement a sieve algorithm for lucky numbers. The idea is to show one possible way to implement a function that has a time complexity of little o of n.

Oulala il fait pleins d'erreurs: du O(log(n)) c'est bien du o(n) , (comme un carré est également un rectangle) . Et l'algorithme qu'il donne ensuite a l'air d'être un mix avec le crible d'erathosthène pour les nombres premiers mais là ça n'a rien à voir puisque un multiple d'un lucky number peut également être lucky (6 * 3 = 18 : 6 et 18 sont lucky) .