Principes et fondements de l'ésotérisme

Il n'y a pas de jugement là-haut, ça n'a aucun sens, sauf pour des entités qui voudraient notre soumission consentie, je dis ça je ne dis rien.

Pas besoin d'atteindre la mort ou d'autres dimensions ou plan d'existence pour trouver des entités donnant leur soumission consentie

Tu n'as pas bien compris ce que j'ai dit.

Il n'y a pas de jugement là-haut, ni de l'âme, ni de l'individu, ou quoi que ce soit d'autre, ça n'a pas de sens. Sauf si des entités malveillantes voudraient nous contrôler et nous soumettre.

Le 11 mars 2023 à 21:03:35 :

Il n'y a pas de jugement là-haut, ça n'a aucun sens, sauf pour des entités qui voudraient notre soumission consentie, je dis ça je ne dis rien.

Pas besoin d'atteindre la mort ou d'autres dimensions ou plan d'existence pour trouver des entités donnant leur soumission consentie

Tu n'as pas bien compris ce que j'ai dit.

Il n'y a pas de jugement là-haut, ni de l'âme, ni de l'individu, ou quoi que ce soit d'autre, ça n'a pas de sens. Sauf si des entités malveillantes voudraient nous contrôler et nous soumettre.

Si j'ai bien compris mais ma réponse était ironique. Je ne crois personnellement pas au jugement des âmes tel que décrit par Pythagore. C'est simplement une présentation de son côté ésotérique en vue d'un autre chapitre.

En revanche ce que tu avances n'est également qu'une théorie.

Je poste bientôt la suite.

La réduction théosophique

La réduction théosophique (du grec : theos, divin et sophia, sagesse) correspond à la numérologie actuelle à 9 nombres. Elle consiste à réduire tous les nombres formés de deux ou plusieurs chiffres à des nombres à un seul chiffre, et cela en additionnant les chiffres qui composent le nombre jusqu’à ce qu’il n’en reste plus qu’un.

19 = 1 + 9 = 10 = 1 + 0 = 1

La réduction théosophique était une opération familière aux pythagoriciens qui négligent les nombres supérieurs à 10. C’est pour cela qu’ils réduisirent aux neufs premiers nombres les nombres supérieurs à 10, ne tenant compte que de leur racine ou pythmên, c’est-à-dire en leur substituant le reste de leur division par neuf, ou le nombre neuf même quand le nombre était un multiple de neuf.

Arthuro Reghini Les Nombres Sacrés dans la Tradition Pythagoricienne Maçonnique

Dans le tableau ci-dessous, tous les nombres d’une même colonne ont la même réduction (première ligne). Par exemple les nombres de la première colonne aboutissent tous au nombre-réduit 1 :

La loi des ternaires

De même que l’univers est divisé en trois mondes : le monde naturel, le monde humain et le monde divin, de même l’homme se compose de trois éléments distincts mais fondus l’un dans l’autre : le corps, l’âme et l’esprit. La Triade ou loi du ternaire est donc la loi constitutive des choses et la véritable clef de la vie.

Pour comprendre ce principe nous devons tout d’abord nous pencher sur la Loi de l’inversion des polarités. La circulation de l’électricité dans nos foyers nous permet tous de savoir qu’il existe un pôle positif, un second négatif et le troisième dit « neutre » ou « terre ».

La loi d’inversion des polarités nous montre que la vie se propage grâce à une pôle actif qui va se « déverser » sur un pôle négatif par le biais d’un pôle neutralisant.

Prenons un exemple simple, une violoniste se produit face à son public :

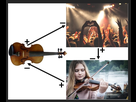
• Le violon est passif (récepteur) par rapport au violoniste mais actif (émetteur) par rapport aux oreilles du public.

• Le public est passif (récepteur) par rapport aux sons du violon mais actif (émetteur) par rapport aux applaudissements qu’il crée.

• Le violoniste est passif (récepteur) par rapport aux applaudissements du public mais actif (émetteur) par rapport à son violon.

Dans ce cas, la force « neutralisante » est l’atmosphère ambiante qui véhicule les ondes et leurs résonances.

Les exemples d’inversion des polarités sont aussi nombreux que la diversité de l’univers.
Les divers courants spirituels ont abordé la question, chacun avec leurs propres langage imagerie et stratégies envers leurs citoyens et/ou adeptes. De l’orient à l’occident, voici quelques exemples de trinités sur lesquelles reposent bon nombre de croyances et/ou de dogmes, mais sur lesquelles il est bon de méditer pour en trouver les analogies…

DE GAUCHE A DROITE ET DE HAUT EN BAS, L’ON RECONNAIT :

• LA SAINTE TRINITE CHRISTIQUE : PERE FILS ENTOURANT LA COLOMBE DE L’ESPRIT.
• BRAHMA, VISHNU ET SHIVA.
• ISIS, OSIRIS ET LEUR FILES HORUS.
• L’HERMES TRISMEGISTE BICEPHALE RETROUVE A FREJUS. SYNTHESE DU TERNAIRE PASSE (VISAGE AGE) FUTUR (VISAGE JEUNE) PRESENT QUI JOINT LES DEUX VISAGES.
• LE YIN (NOIR) ET LE YANG (BLANC) ; INDISSOCIABLEMENT UNIS DANS LE CERCLE DE L’UNIVERS ET DE LA VIE.

Quelques autres exemples de ternaires

Pythagore, inventeur du terme « cosmos », qualifiait les Trois Mondes à travers les termes suivants :

• Monde des Archétypes (devenus par la suite le Monde des Idées avec Platon)
• Microcosme, ou petit monde, l’Homme
• Macrocosme, le grand monde, l’Univers

On retrouve une parenté entre les Trois Mondes et la psychologie des profondeurs de Carl Gustav Jung.

• Le Monde des Archétypes s’apparent au domaine du Soi, à la vision la plus élevée que l’on se fait de Soi.
• Le Microcosme correspond à l’être conscient, le Moi, qui s’exprime à travers ses pensées, ses sentiments et ses actions.
• Enfin le Macrocosme représente le terrain d’expérimentation du Moi à travers le Je agissant dans l’espace-temps, la matière, auprès de la collectivité, des autres au sens large.

Carl Gustav Jung définit les archétypes de cette manière :

Au-delà de l’inconscient personnel nous avons l’inconscient collectif qui est d’une qualité et d’une structure entièrement différentes, quelque chose de jamais acquis ; c’est né avec nous, venu au monde avec nous, apparu à l’intérieur de notre structure cérébrale ; c’est quelque chose qui est identique à la structure des instincts, qui a la forme d’un instinct, et fonctionne à l’image d’un instinct ; nous appelons ces « images » des archétypes. »

Carl Gustav Jung - Psychologie et alchimie

On retrouve ce concept des Trois Mondes un peu partout sur le globe depuis la nuit des temps, seules les appellations changent. Cette classification qui correspond également au ternaire Dieu, l’Homme et l’Univers existe depuis que l’homme a cherché à organiser ses idées selon un procédé classificatoire. On parle aussi de Monde Spirituel, Monde Psychique et Monde Physique et plus généralement d’esprit, d’âme et de corps.

Chacun des neuf premiers nombres est relié à l’un de ces Trois Mondes, ou mieux encore, chaque triplet de nombres représente un monde en soi. Il devient alors possible d’interpréter un nombre en fonction du lieu qu’il occupe dans la matrice.

Chaque nombre répond, en effet, à une idée et à un hiéroglyphe caractéristique, si bien que les lois des combinaisons des nombres vérifient la combinaison des symboles et des idées. (…) Cette loi est une des meilleures clefs pour ouvrir les mystères antiques.

Édouard Schuré - Les Grands Initiés

Le 11 mars 2023 à 23:36:13 :
Je fav le topic merci craie

Je t'en prie. Avec grand plaisir.

3 Géométrie de la matière

Les sons créateurs de formes et la cymatique

Lorsqu'une plaque sur laquelle on a déposé du sable ou un liquide est soumise à une vibration ou à un son, le sable ou le liquide s'arrangent en d'extraordinaires figures géométriques. Ces figures sont segmentées en cellules symétriques d'autant plus fines et complexes que la fréquence vibratoire est élevée. Des gouttes d'eau isolées pulsent et s'organisent en polyèdres.
Par ce procédé, le son est transcrit en formes. La voix humaine produit de merveilleuses figures et l'on peut suivre les formes d'une musique. Beaucoup de ces figures acoustiques sont analogues à des formes que l'on trouve dans les végétaux et les animaux, et aussi dans les planètes et les crop-circles.

Les sons peuvent-ils se manifester par des formes ?
Compte tenu de leur immatérialité, cela ne semble guère possible. Ils se propagent partout dans l'espace de façon invisible. Toutefois, si on leur prête un peu plus attention, on remarque qu'un son possède une structure qui se déroule dans le temps. Il a un début, un rythme et une fin et nous pourrions parfois dessiner cette forme qui se déploie dans l'espace. Il semble naturel que des structures rythmiques inscrites dans le temps puissent avoir des correspondances avec des structures géométriques inscrites dans l'espace. Nous allons explorer comment s'effectue cette correspondance et dans quelles conditions.

• LA PREMIERE IMAGE REPRESENTE UN FILM D'EAU DEPOSE SUR UNE MEMBRANE RONDE EN LATEX SOUMISE A UNE VIBRATION DE 19 HERTZ, ECLAIRE PAR UNE LAMPE INSTALLEE AU-DESSUS. ON VOIT EN BLANC LES REFLETS DE L'ECLAIRAGE (PHOTO ERIK LARSON)

• LA DEUXIEME IMAGE REPRESENTE UNE GROSSE GOUTTE D'EAU DEPOSEE SUR UNE SURFACE PLATE SOUMISE A UNE VIBRATION DE QUELQUES DIZAINES DE HERTZ, ECLAIREE PAR UNE LAMPE INSTALLEE AU-DESSUS. (PHOTO ALEXANDER LAUTERWASSER, IMAGES SONORES D'EAU)

• LA TROISIEME IMAGE REPRESENTE UNE PLAQUE OVALE EN ACIER, DE LONGUEUR 23 CM, SUR LAQUELLE ON A DEPOSE DU SABLE FIN ET QUI VIBRE A 12'301 HERTZ. ON VOIT EN BLANC LA FIGURE DESSINEE PAR LE SABLE (PHOTO ALEXANDER LAUTERWASSER, IMAGES SONORES D'EAU)

Si nous frappons une plaque métallique mince, posée de telle sorte qu'elle ne soit pas amortie par un contact, elle se met à vibrer pendant un moment. Généralement cela produit un son qui est soit un bruit soit quelque chose de plus musical, une note continue. Puis la vibration s'atténue et s'arrête.
Il existe un procédé facile à mettre en œuvre pour VOIR les vibrations de la plaque. Il consiste à saupoudrer la plaque avec une poudre fine : sable, sel ou semoule, par exemple.

Il y a différentes façons de faire vibrer la plaque. Lui donner un choc ne suffit pas car la vibration s'éteint rapidement. Il faut que la vibration soit entretenue pour que les grains de poudre aient le temps de se déplacer et de s'organiser.

Une méthode simple est de placer la plaque au-dessus d'un haut-parleur, dont on peut faire varier à volonté la hauteur du son émis. On peut aussi utiliser un vibreur électromagnétique, sort de haut-parleur sans membrane, alimenté par un générateur électronique de courant.
Sous l'effet des secousses transmises par le son, les grains se déplacent comme lorsqu'on secoue légèrement un tapis. Ils se rassemblent dans les endroits les plus calmes et y forment des lignes. Pour certaines fréquences précises, les lignes divisent la plaque en cellules souvent symétriques et dessinent des figures géométriques impressionnantes.

Nous allons explorer ces figures de plus près. Pour cela, nous profiterons des observations des pionniers de ce domaine, Chladni, Waller, Jenny et Lauterwasser. Ils les ont mis en évidence, en ont été émerveillés et passionnés.
Pour mieux comprendre ce qui se passe quand une plaque se met à vibrer, faisons l'expérience avec un objet plus simple, une corde. Plus simple parce qu'une plaque vibre à la fois dans sa longueur et sa largeur (en 2 dimensions) alors qu'une corde ne vibre qu'en longueur (une seule dimension). De plus la vibration de la plaque rigide est très petite et difficilement visible à l’œil nu alors que celle de la corde est bien visible.

Observons donc une corde sur une guitare que l'on excite en la poussant ou pinçant. Elle émet une note. Pendant que le son est émis, nous la voyons effectuer des mouvements rapides de haut en bas. Ils sont si rapides que notre œil ne peut pas les suivre et que nous voyons un fuseau. En réalité, la corde passe alternativement d'une position (représentée en bleue sur la figure ci-dessous) à une autre (représentée en rouge). La forme globale de fuseau provient de l'impression durable que produit l'image sur notre rétine.

FORMES CREEES A DIFFERENTES FREQUENCES DE RESONANCE. LES FREQUENCES SONT EN RAPPORT SIMPLE. 2 FOIS PLUS GRANDE POUR FAIRE 3 FUSEAUX.

ONDE STATIONNAIRE DE 3 FUSEAUX SUR UNE CORDE TENDUE ENTRE 2 SUPPORTS. LE SUPPORT DE DROITE EST AGITE PAR UN MOTEUR. CORDE D'1,5 M, ENDUITE DE CRAIE FLUORESCENTE.

Afin d'observer ces fuseaux plus aisément, nous transposons donc cette expérience sur une corde tendue entre deux supports. L'un des supports est agité verticalement par un moteur (comme une main qui agite une corde à sauter, mais l'agitation reste dans le plan vertical, on ne fait pas tourner). Cette agitation est entretenue. On peut choisir la vitesse d'agitation et sa force (son amplitude).
Plus on agite vite, plus on fait d'allers et retours par minute ou par seconde. Le nombre d'allers - retours par seconde s'appelle la fréquence. Elle est exprimée en Hertz (abréviation Hz).
Ici, on ne s'occupe pas de savoir si la vibration produit ou non un son comme une corde de guitare. On peut toutefois dire qu'elle sera peut-être audible si sa valeur est située parmi les fréquences audibles de l’oreille humaine.

Commençons par agiter la corde lentement et augmentons la vitesse progressivement. Pour une certaine fréquence qui reste faible, et uniquement pour cette fréquence, nous obtenons un seul fuseau. Même si le fuseau reste globalement à la même position, la corde n'a rien d'immobile. Mais le mouvement a lieu sur place. On dit qu'il est stationnaire.
Si nous augmentons la fréquence, nous perdons cette forme stationnaire et l'agitation devient chaotique. Continuons à augmenter la fréquence. Brusquement, une deuxième forme stationnaire prend place avec 2 fuseaux, puis une autre avec 3, etc.

SOUS L'ACTION DE LA VIBRATION D'UN CRISTAL SUR UNE PLAQUE (7560 HZ), LE SABLE BOUGE ET SE MET EN PLACE PEU A PEU (DE HAUT EN BAS) JUSQU'A FORMER UNE FIGURE STATIONNAIRE.

Les fuseaux ont une position fixe sur la corde, car les points entre deux fuseaux, appelé nœuds par les physiciens, sont quasi-immobiles. On pourrait y déposer une fourmi sans qu'elle soit trop dérangée. En revanche entre ces nœuds, la corde oscille de haut en bas et de bas en haut. En plein centre d'un fuseau, c'est l'agitation maximum, c'est un ventre. Plus forte est l'agitation, plus grande est l'amplitude du ventre.
Les valeurs des fréquences qui créent les fuseaux sont spéciales. On les appelle des fréquences harmoniques.
Revenons maintenant aux plaques métalliques et à leurs figures acoustiques. Observons d'abord comment se forme une figure acoustique. Prenons une plaque carrée que nous saupoudrons de sable fin. Quand nous mettons le vibreur en route, la poudre se met à bouger, s'écoule, se rassemble peu à peu à certains endroits. Augmentons lentement la fréquence. La poudre bouge encore, des courants apparaissent, elle s'organise. Puis, pour une fréquence particulière, une figure géométrique se forme nettement.

UNE FIGURE OBTENUE SUR UN TONOSCOPE EN PRONONÇANT LA VOYELLE A.

Les lignes où le sable se rassemble sont des zones calmes, l'équivalent des nœuds de la corde. Ce sont les lignes nodales. Ailleurs, la plaque oscille verticalement. La formation de ces figures est l'indication que des ondes stationnaires se sont établies dans la plaque. Les figures acoustiques obtenues sont extrêmement variées.

SUITE DE FREQUENCES RESONNANTES

Si nous augmentons progressivement la fréquence de vibration, plusieurs figures géométriques apparaissent successivement et soudainement. Ces figures sont toutes différentes. Toutefois, on y retrouve souvent un même motif de base. Les figures géométriques n'apparaissent que pour certaines valeurs précises des fréquences de vibration.
Les fréquences graves produisent des figures simples. Plus la fréquence est élevée, plus le nombre d'éléments qui composent la figure est grand. Ces éléments sont donc de plus en plus petits. Les lignes sont de plus en plus rapprochées et de plus en plus fines.

LÉGENDE : IMAGES SONORES D'EAU
FIGURES ACOUSTIQUES APPARAISSANT POUR DES FREQUENCES CROISSANTES, DE GAUCHE A DROITE ET DE HAUT EN BAS. LE CHIFFRE INSCRIT VERTICALEMENT A DROITE DE CHAQUE FIGURE DONNE LA FREQUENCE EN HZ, DE 196 A 16357. LE CHIFFRE INSCRIT EN-DESSOUS A DROITE INDIQUE LE RAPPORT ENTRE 2 FREQUENCES SUCCESSIVES.

Lauterwasser a apporté une contribution remarquable dans l'étude et la contemplation des formes créées au sein de l'eau par les vibrations sonores. Il prend une coupelle de plusieurs centimètres de diamètre, la remplit d'eau sur une épaisseur de quelques millimètres, et la pose avec minutie sur un vibreur électromagnétique. L'eau se met en mouvement. Des courants, des crêtes, des creux, des tourbillons naissent et forment des structures.

Mais comment délimiter des formes dans l’eau ? Où tracer des lignes ? C'est la lumière d'éclairage elle-même qui se charge de les dessiner, grâce à sa réflexion sur l'eau. Une lampe est installée au-dessus de la coupelle, et une caméra filme la surface de l'eau. Lorsque les conditions sont finement réglées, des figures stationnaires se forment. La coupelle doit être parfaitement horizontale et l'épaisseur de l'eau doit être ajustée. Puis, pour obtenir une figure symétrique aux oscillations régulières, il faut moduler l’intensité et la fréquence.

Les parties claires sont celles qui renvoient la lumière vers la caméra. Ce sont essentiellement les crêtes des vagues. Elles se présentent comme des lignes fines. Les vallées aussi sont claires, mais moins, et elles sont aussi plus larges. Les parties noires sont les pentes entre crêtes et vallées. Comme pour le sable, on a un entrecroisement de structures annulaires et de structures radiales.

Lorsqu'on monte doucement en fréquence, grâce au soin pris pour mettre en place le dispositif, on voit apparaitre une grande variété de superbes figures symétriques avec des structures radiales. Le nombre des rayons ou des secteurs est surprenant. On y voit aussi bien des structures simples d'ordre 2, 3, 4, 6, 8, 12, 16 ou 24, mais également des ordres comme 5, 7, 10, 14 ou 18 branches.
Si on épaissit le liquide, par exemple avec de la glycérine, les figures s'ordonnent en réseau, à la façon d'un cristal.

Les films d'eau sont sensibles aux sons d'une musique. Les formes suivent le rythme et la mélodie de la musique. Pour A. Lauterwasser, ces images-là sont les plus fascinantes et les plus vivantes parce que les figures changent à chaque seconde.

Jenny a également exploré l'effet des vibrations sur des gouttes de liquides les plus variés : eau, huile, alcool, essence, alcool. Lauterwasser s'est plongé dans le monde des gouttes d'eau. Les liquides transparents sont éclairés avec une lampe placée par dessous ou par-dessus, observés et photographiés par-dessus.
Au début de la mise en marche de la vibration, des cercles concentriques se forment. Ils ne sont pas immobiles, mais parcourus par un mouvement constant. L'eau se déplace du centre vers la périphérie puis revient au centre.

Lorsque l'on augmente l'intensité ou la fréquence vibratoire, des figures géométriques apparaissent brusquement. Puisque les lignes correspondent aux crêtes et protubérances, elles soulignent le relief de la goutte. Des protubérances naissent, s'affaissent et d'autres naissent là où étaient les creux. Un rythme de pulsation s'établit. Ces changements ne sont pas synchronisés avec la vibration. Les photos montrent des instantanés de ces mouvements.
Pour certaines plages de fréquences précises, la goutte se segmente en cellules qui dessinent des polygones : TRIANGLE, QUADRILATERE, PENTAGONE, HEXAGONE, HEPTAGONE, DECAGONE et autres. Ces polygones oscillent et le point d'un sommet par exemple passe sans cesse de l'état élevé à l'état affaissé. Il suffit d'une petite variation de fréquence pour modifier la forme. Il n'existe pas de relation entre le nombre de côtés du polygone et la fréquence.

Aspects géométriques et sonores de l’univers

Au commencement

Loin d'être dues au hasard, les formes de l'univers sont sous-tendues par des trames géométriques. On constate leur présence depuis l'atome jusqu'aux amas de galaxies, en passant par les plantes, les animaux, les circuits énergétiques de la Terre, et même le corps humain. Ces géométries sont intimement liées à des fréquences sonores. Sons et géométries sont l'expression manifestée de schémas directeurs sous-jacents et trouvent de parfaites similitudes avec la géométrie du son présenté précédemment.

Les scientifiques nous affirment que l'univers est né à partir d'un point microscopique qui a explosé dans un immense Big Bang. Au fur et à mesure que l'énergie de l'explosion s'est propagée, elle a occupé de plus en plus de volume. En même temps, sa température a décru, et sont apparues les forces fondamentales de la gravité et de l'électromagnétisme, puis les éléments de matière : particules, atomes, puis enfin étoiles et planètes. Sur une planète spéciale, la Terre, la vie s'est développée sous forme de bactéries, puis de plantes et d'animaux, et enfin d'êtres humains.

Dans cette évolution, ce qui aurait présidé à l'apparition des magnifiques formes de la matière et de la vie, c'est le plus pur des hasards. Au hasard des rencontres, des associations d'éléments se font et se défont. Les associations les plus fortes, les plus stables, et celles douées d'un pouvoir de croissance et de reproduction, auraient pris de la place au détriment des autres, par un mécanisme de sélection naturelle.
Ce scénario n'est pas la transcription d'observations directes. C'est un modèle hypothétique, élaboré pour rendre compte des rudiments d'observations astronomiques que les astrophysiciens ont collectées depuis notre petit coin d'univers, la Terre, et son environnement spatial proche, avec nos instruments dont la technologie est admirable, mais limitée.

Les astrophysiciens adhèrent massivement à cette théorie. Ce qui surprend et nous interroge dans ce scénario, c'est comment une explosion brutale, sans finalité ou sans guide de conduite, aurait pu donner naissance à toutes les lois physiques minutieusement réglées de notre univers et à la profusion des formes de vie que nous observons. Les physiciens eux-mêmes ont été frappés par le fait que les constantes fondamentales de la physique (charge de l'électron, constante de la gravité, vitesse de la lumière, etc.) sont ajustées avec précision pour assurer les conditions de la vie. C'est ce qu'ils ont nommé le principe anthropique (à ne pas confondre avec le principe de l'entropie). Les formes de vie, qui font preuve d'énormes capacités d'adaptation aux changements dramatiques de l'environnement, nous démontrent à quel point elles sont régulées par d'extraordinaires mécanismes de fonctionnement. Tous ces phénomènes ne seraient-ils pas le fruit d'une intelligence ? Ou tout au moins d'une science supérieure ?
À ceux qui émettent des doutes sur la valeur de la théorie du Big Bang, les scientifiques répliquent que c'est la seule théorie valable et qu'elle est acceptée par tous. Ceux qui ne sont pas convaincus par l'emploi des lois du hasard, sont soupçonnés de réintroduire le principe du finalisme ou téléologie qui a été laborieusement abandonné au 19e siècle par les efforts de la science, et de faire appel à une intelligence créatrice (Dieu) dans leur scénario. Autrement dit, un opposant au scénario scientifique standard du Big Bang s'expose à être taxé de complicité avec le créationnisme, ce qui pour un scientifique est un manquement grave à la science. Les créationnistes prennent le texte biblique à la lettre sur le plan matériel, niant sa valeur symbolique. Selon eux par exemple, la Terre aurait été créée en 6 jours et serait âgée de 6000 ans.

En-dehors de ces deux positions extrêmes, le tout-hasard ou la création en 6 jours, n'y aurait-il pas d'autres voies envisageables, d'autres scénarios de création ?
Le but n'est pas de polémiquer sur l'opposition entre la théorie scientifique cosmologique actuelle et le créationnisme. Il est de proposer un autre regard, un autre type de scénario. Ce scénario n'est pas inventé à partir de rien. Il résulte de la convergence d'observations scientifiques concernant les aspects géométriques de l'univers, et d'enseignements traditionnels sur la description du cosmos et de sa création. Cette convergence nous amènera à une vision renouvelée de l'Homme et de son rapport avec le cosmos. C'est une vision cohérente, qui d'une part donne du sens aux mythes et aux légendes, et qui d'autre part redonne à l'Homme sa place dans l'univers.
Nous entamons notre investigation en examinant comment des trames géométriques sont décelables à tous les niveaux de la nature, depuis l'atome jusqu'aux galaxies. Tout d'abord, observons notre environnement proche.

TRAMES GEOMETRIQUES DANS LA NATURE
En portant notre attention sur les plantes et les animaux autour de nous, nous découvrons que la nature revêt une grande variété de formes, qui sont généralement arrondies et plutôt irrégulières. Rien ne semble y être géométrique. Pourtant, des structures géométriques sous-tendent en filigrane la plupart des formes naturelles.

SIMILITUDES GEOMETRIQUES DANS LA NATURE

LES POLYEDRES

Le qualificatif de géométrique nous suggère en premier lieu des carrés, triangles, et autres polygones plus ou moins rég uliers, faits de segments droits avec des angles vifs.
C'est bien cet aspect que nous reconnaissons dans les cristaux. Lorsque nous observons des concrétions de calcite ou de quartz, nous constatons qu'elles sont délimitées par des facettes planes régulières. Ces facettes se coupent selon des angles vifs dont les valeurs ne sont pas quelconques, mais déterminées par des symétries. Les facettes planes déterminent des cubes, des prismes, ou d'autres volumes plus complexes à faces planes appelés polyèdres. On trouve aussi de telles géométries régulières cristallines dans de nombreux autres minéraux et dans les cristaux de glace.
Grâce à la découverte des rayons X en 1895 et à celle du phénomène de leur diffraction par les substances cristallines en 1912, les scientifiques ont pu déterminer que les cristaux étaient constitués d'un empilement périodique et régulier de motifs élémentaires composés de quelques atomes. Ce motif appelé maille a la forme d'un polyèdre, cubique, prismatique ou parallélépipédique. On a pu dénombrer 14 modèles différents de polyèdres compatibles avec un empilement régulier.
Même si cela semble moins apparent, on trouve également des formes polyédriques chez les animaux et les plantes. Citons les carapaces des tortues ou de crustacés, les cuticules ou les yeux de certains insectes. Quant aux fleurs, nombreuses sont celles qui s'épanouissent en une belle étoile régulière. Les étoiles sont elles-mêmes des polygones dont les angles sont rentrants.

SPIRALES

Chez les plantes et les animaux, une observation attentive nous révèle qu'il existe beaucoup de formes géométriques autres que les polyèdres. Les formes en courbes constituent un deuxième type de géométrie abondantes dans la nature. Les spirales en sont les représentantes les plus remarquables. On en a des exemples dans les coquilles d'escargots ou les cornes de bélier.

Les galaxies se développent également selon une logique de spirale

Dans les plantes, leurs éléments (feuilles, fleurs, épines, écailles) s'étagent le long de la tige selon une construction élaborée au cours de la croissance. Cette construction se présente selon deux modes différents. Dans l'un, les éléments sont disposés par groupes de deux l'un en face de l'autre. Dans l'autre, ils naissent l'un après l'autre et se placent en spirales tout autour de la tige.

Dans le cas de la spirale, on constate que les éléments sont placés les uns par rapport aux autres selon un angle dont la valeur est 137,5°. Or cette valeur est celle qui partage la circonférence 360° selon le nombre d'or 1,618. À cause de cette proportion, le nombre de spirales que l'on peut dénombrer dans ces plantes prend des valeurs particulières.

Par exemple, dans une fleur de tournesol, la disposition des fleurons laisse apparaitre de nombreuses spirales. On peut en dénombrer 21 dans un sens et 34 dans l'autre, ou encore 34 et 55, ou 55/89 ou 89/144.
Dans un ananas, on peut trouver 8 rangs de fleurons dans un sens et 13 dans l'autre. Dans la pomme de pin, 8 rangs d'écailles dans un sens et 13 dans l'autre ou encore 2 et 3, ou 3/5, 5/8 ou 8/13. Dans la marguerite 21/34 et dans le céleri, 1/2.
Or tous ces nombres font exactement partie de la suite étudiée par le mathématicien italien LEONARDO FIBONACCI (vers 1175 - vers 1250) :
1, 2, 3, 5, 8, 13, 21, 34, 55, 89
Le nombre d'or y transparait dans le rapport de deux de ces nombres consécutifs.

FRACTALES

Les structures en arborescence, telles que celle d'un arbre, faites de grosses branches qui se ramifient en petites, qui elles-mêmes se ramifient en rameaux, etc. peuvent être décrites comme des structures fractales. C'est un troisième type de géométrie qui ne ressemble ni aux polyèdres ni aux spirales.
Les fractales sont des images de synthèse à 2 ou 3 dimensions comportant des ensembles de points, de lignes, ou de surfaces obtenues par la répétition d'un processus de construction graphique ou mathématique. À chaque étape de répétition est associée une réduction (ou augmentation) d'échelle qui confère aux images obtenues un aspect fragmenté, ramifié ou poreux, qui est identique quelle que soit l'échelle d'observation.

LE CHOU ROMANESCO EST L’UNE DES PLUS BELLES FRACTALES DE LA NATURE

LES FLOCONS DE NEIGE ET LEURS FORMES FRACTALES

LA FOUGERE SE DEVELOPPE EGALEMENT SELON UN MODELE FRACTALE

LE CORAIL EST EGALEMENT UNE FORMATION FRACTALE RAPPELANT L’ARBRE

TOUT COMME LE SYSTEME SANGUIN DU CORPS HUMAIN

Des structures fractales sont sous-jacentes dans des formations naturelles d'apparence irrégulière. On les rencontre dans les réseaux fluviaux, dans la forme déchiquetée des montagnes et dans les formations nuageuses. On en découvre dans la matière fragmentée, découpée, poreuse, filamenteuse. La preuve qu'une structure fractale est sous-jacente à ces formations est qu'il est possible de les simuler graphiquement de façon réaliste par des images fractales de synthèse. C'est par exemple le cas des fougères, des montagnes, des nuages et de beaucoup d'autres matières et paysages.

RAPIDE RESUME

Nous avons mis en évidence que des géométries, polygones ou polyèdres, spirales et fractales, constituent une armature sous-jacente des formes de la nature. Mais ces trames sont souples et vivantes, une armature n'est pas rigide. Plastique et vivante, la géométrie peut subir des adaptations par rapport à sa forme idéale parfaitement symétrique. On peut se figurer ce caractère en considérant une tente qui prend des aspects bancals si elle est installée sur un terrain irrégulier. Cela ne lui enlève pas sa conception de fabrication avec des armatures parfaitement symétriques et ajustées. Même si elle est installée de travers, sa géométrie parfaite d'origine reste toujours manifeste dans sa forme apparente.

SPIRALES ET POLYEDRES DANS LE COSMOS

Quittons la Terre et élevons-nous maintenant dans l'espace sidéral. La représentation généralement acceptée est celle d'un univers en expansion depuis la phase initiale du Big Bang. Cela pourrait nous conduire à imaginer que les étoiles sont parsemées au hasard de façon homogène dans le cosmos, comme des cailloux dans un champ. Or ce n'est pas le cas. Allons-nous y trouver des trames géométriques ?

GALAXIES

Les milliards de milliards de milliards d'étoiles qui peuplent le cosmos ont tendance à s'agglomérer en paquets de dizaines ou de centaines de milliards d’étoiles : les galaxies. Entre les galaxies, subsistent des espaces relativement vides d'étoiles.
La première galaxie découverte fut celle dans laquelle nous sommes situés, la Voie Lactée. À vrai dire, jusqu'au début du 20e siècle, la Voie Lactée semblait s'identifier à la totalité de l'univers. C'est seulement après le développement des télescopes et des spectroscopes qu'on a pu estimer les distances qui séparent la Terre des étoiles visibles. On a pu évaluer approximativement le diamètre de la Voie Lactée.
En astronomie, les distances sont exprimées en années-lumière (al). Une année-lumière est la distance parcourue par la lumière en un an dans l'espace vide, à la vitesse de 300'000 km/s, soit environ 10'000 milliards de kilomètres. C'est donc une unité de distance, pas celle d'une durée.
La Voie Lactée a la forme d'un disque mince renflé en son centre. Son rayon est estimé à 45'000 années-lumière. Le système solaire se trouve vers l'extérieur, à 26'000 années-lumière du centre, soit environ les 2/3 du rayon.
En 1923, Edwin Hubble découvrit que la nébuleuse d'Andromède est située en-dehors de la Voie Lactée, car il estimait son éloignement à 900'000 al. Or elle était reconnue comme étant elle-même une galaxie. C'est le début de la compréhension qu'il existe de nombreuses galaxies en-dehors de la Voie Lactée. À ce jour, le nombre des galaxies cataloguées est démesuré.

la galaxie spirale ngc 1232, située a 100 millions d'années-lumière et d'un diamètre d'environ 200'000 années-lumière (constellation Eridan)

Certaines galaxies n'ont aucune forme particulière, mais la plupart adoptent des formes géométriques. Un petit nombre sont elliptiques, d'autres lenticulaires. La majorité des galaxies sont remarquablement spiralées.

AMAS DE GALAXIES

Par la suite, les astronomes se sont aperçus que les galaxies n'étaient pas distribuées de façon homogène dans le cosmos, pas plus que les étoiles en leur sein. Elles sont regroupées en amas.
Ainsi, à côté de la Voie Lactée, on trouve la galaxie Andromède, les nuages de Magellan et une quinzaine de galaxies naines. Cet ensemble est appelé le groupe local. Sa taille est de 13 millions d'al (13 Mal), soit environ 130 fois plus grande que celle de la Voie Lactée.
Les galaxies sont assemblées en groupes, et les groupes sont assemblés en amas qui englobent à la fois des groupes de galaxies et des galaxies isolées. Avec une taille moyenne de 60 Mal, les amas sont environ 5 fois plus grands que les groupes.

SUPER AMAS

Si nous montons encore plus haut dans l'échelle des distances, nous nous apercevons que les amas aussi ne sont pas distribués de façon aléatoire. Les voilà regroupés en super amas. Un super amas inclut environ 5 ou 6 amas, et a une taille moyenne d'environ 260 Mal, soit 4 fois plus qu'un amas. Par exemple, le groupe local contenant la Voie Lactée est inclus dans le superamas de la Vierge, également appelé superamas local. Il a été découvert par l'astronome Gérard de Vaucouleurs en 1960.

L'UNIVERS EN EPONGE

À ce stade de notre exploration, nous avons reconnu 3 niveaux hiérarchiques d'agglomération de galaxies (groupe, amas et superamas). Croyez-vous que cette architecture cosmique s'arrête à cette échelle ? Ce n'est pas le cas, et le plus étonnant est à venir.
En effet, les superamas ont tendance à se rassembler en de vastes filaments longs et minces, ou en feuillets ressemblant à des crêpes. Ces feuillets et ces filaments délimitent de grands espaces vides, comme s'ils étaient placés à la surface de bulles de savon vides. Les bulles de vide cosmique occupent une place prépondérante. Elles ont une taille estimée à 650 Mal, mais certains filaments peuvent être bien plus longs. Quant au vide, il n'est pas réellement vide, mais peuplé de galaxies isolées et d'un gaz ténu.
Avec ces bulles, le cosmos prend l'aspect d'une structure cellulaire. Les cellules (les bulles) sont analogues aux cavités d'une éponge, avec des galeries qui relient les cavités. C'est pourquoi on parle de la structure en éponge de l'univers.
La géométrie cellulaire de l'univers a été découverte dans les années 1990. Elle a surpris les astronomes, car aucun modèle issu de la théorie standard du Big Bang ne pouvait l'expliquer.

Le super amas de la Vierge

L'univers en éponge

LES POLYEDRES QUI STRUCTURENT LA TERRE

Entre l'infiniment grand et l'infiniment petit, revenons à notre planète Terre, en l'envisageant dans sa globalité sphérique. En elle-même, la forme sphérique de la Terre, constitue à l'évidence une géométrie. Son axe de rotation en est un élément supplémentaire essentiel. Mais c'est une autre géométrie que nous allons aborder. Nous allons découvrir que la Terre est architecturée par une trame géométrique, qui n'est visible que par un examen attentif. Et nous y retrouverons les polyèdres de Platon.
Puisque les polyèdres sont définis par des lignes droites, nous pouvons nous attendre à déceler ces lignes à la surface de la terre. En effet, elles sont mises en évidence par des alignements ponctués par des sites sacrés. L'un des pionniers de l'étude des alignements de sites sacrés a été l'anglais Alfred Watkins vers 1920. Dans la campagne du Sud de l'Angleterre, il observa que des sites sont fréquemment alignés sur des kilomètres. Il nomma ces lignes « Lignes de Ley ».
Les sites ainsi pris en compte sont des pierres levées (menhirs), des collines rondes artificielles, des tumuli, des sources sacrées ou encore des églises. D'autres chercheurs se rendirent compte que de telles lignes existaient aussi en Europe et en Amérique. En se recoupant, elles déterminent des triangles, des hexagones et d'autres polygones, dont le réseau couvre la planète entière en une sorte de grille.

Une ligne de ley a saintbury, angleterre. elle emprunte un ancien chemin, passe par une croix medievale, une eglise saxonne, et un tumulus

Ces lignes fonctionnent à la manière de canaux ou de vaisseaux qui conduisent l'énergie vitale de la planète, de la même manière que le corps humain est irrigué par d'innombrables vaisseaux, les nadis et méridiens d'acuponcture décrits par les textes védiques. La grille constitue une armature qui alimente la planète en flux vitaux indispensables à sa propre vie et à celle de ses habitants de tous les règnes (plantes, animaux, humains, minéraux).

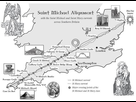
Alignement de Saint Michel en Grande Bretagne

La majorité des constructions sacrées sont implantées soit sur ces lignes, soit sur leurs croisements (les sommets des polygones), à cause de l'énergie vibratoire spéciale qui émane de ces lieux. Les monuments sacrés ont plusieurs fonctions. Ils collectent et régulent l'énergie qui s'y manifeste. À cause de ces énergies spéciales, les nœuds ou croisements de la grille sont fréquemment le siège d'anomalies magnétiques ou géophysiques, ou encore de manifestations climatiques particulières. Certains d'entre eux ont acquis une réputation sinistre comme le triangle des Bermudes ou le triangle du diable au large du Japon.

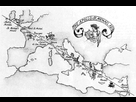
Ligne de ley europeenne traversant les edifices religieux majeurs

Vers 1970, en repérant les emplacements de ces anomalies, trois scientifiques russes, Nikolai Goncharov, Valery Makarov et Vyacheslav Morozov, mirent en évidence l'existence d'un réseau planétaire principal, qui est architecturé par des polyèdres. Par la suite, vers 1983, ce réseau fut complété et ajusté par un couple américain, le Dr William Becker et son épouse le Dr Bethe Hagens.

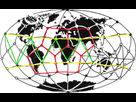
La grille planetaire de goncharov, makarov et morozov en vert, l'icosaedre, en rouge le dodecaedre

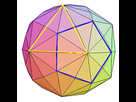
Le polyedre a 120 triangles de la grille planetaire de becker-hagens

Dans la même logique Ivan Sanderson,biologiste aux États-Unis, créateur de la Society for the Investigation of the Unexplained, a également apporté une contribution à l'étude de la grille planétaire dans un article publié en 1972 dans Saga magazine: « Les 12 vignes du diable autour du monde ».
Il y rapporte les résultats de ses investigations sur les zones d'anomalies terrestres : anomalies magnétiques, aberrations énergétiques, distorsions du temps, disparitions de bateaux et d'avions et autres phénomènes étranges. Pour amasser les données et en faire l'analyse statistique, il tire profit des méthodes modernes électroniques de collecte.

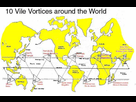
Les 10 triangles presentant des anomalies energetiques

Il met en évidence 12 zones d'anomalie. Le plus étonnant est qu'elles sont équidistantes et disposées de façon régulière autour du globe. Deux d'entre elles sont les pôles et les 10 autres zones sont réparties de part et d'autre de l'équateur. Les 3 plus connues sont le triangle des Bermudes dans les Bahamas, le triangle de la Mer du diable au Japon et le triangle d’Hawaï.

GEOMETRIE DES PLAQUES TECTONIQUES

Les polyèdres qui sous-tendent la planète se manifestent parfois en guidant les mouvements de la croûte terrestre. C'est le cas des déplacements des plaques tectoniques. De quoi s'agit-il ?
Lorsque nous observons une carte géographique des continents, nous sommes frappés par la similitude des profils de la côte Est de l'Amérique du Sud et de la côte Ouest de l'Afrique. Si nous pouvions rapprocher ces côtes, il semble qu'elles pourraient s'emboiter parfaitement l'une dans l'autre. C'est ce qu'avait remarqué plusieurs savants dès le 19e siècle. En partant de cette observation, l'allemand Alfred Wegener proposa sa théorie de la dérive des continents en 1912. Il avança que les continents se déplacent très lentement à la surface de la Terre et bougent les uns par rapport aux autres. Ainsi, les côtes africaines et américaines auraient par le passé été assemblées et se seraient séparées ensuite en s'écartant de plus en plus. En remontant le film à l'envers dans le temps, Wegener imagina que tous les continents étaient autrefois réunis en un seul grand supercontinent, la Pangée (Pangaea : Terre totale en grec). Puis la Pangée se serait progressivement disloquée il y a 250 millions d'années. Ses morceaux ont dérivé et se sont fragmentés jusqu'à donner les continents actuels. Plus tard, des scientifiques ont conforté la thèse des continents autrefois réunis en relevant des similitudes entre la faune et la flore de continents éloignés, qui pourraient s'expliquer par les passages qui les auraient reliés par le passé.

Représentation de la dérive des continents

Cette théorie n'obtint pas les faveurs de la communauté scientifique. Il fallut attendre les années 1960 où elle fut renforcée par la théorie de la tectonique des plaques élaborée par Dan McKenzie, William Morgan, Xavier Le Pichon, Robert Parker et John Wilson. Selon cette théorie, les continents sont portés par des plaques de la croute terrestre. Les plaques flottent sur le magma liquide et dérivent les unes par rapport aux autres. Elles s'éloignent, ou se rapprochent et s'entrechoquent, ou encore se frottent l'une contre l'autre. Leur vitesse relative est de quelques centimètres par an. En s'éloignant, elles laissent entre elles un espace qui se remplit d'une nouvelle matière qui surgit des fonds marins et forme des crêtes océaniques. Un exemple de crête est celle du milieu de l'océan Atlantique.
Les bordures des plaques tectoniques sont repérées par les crêtes, les fosses océaniques et les rangées de volcans et d'arcs insulaires. On a dénombré une douzaine de plaques. Mais délimiter des plaques n'est pas si évident et leur nombre est approximatif.

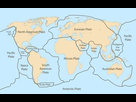
Carte des plaques du plancher oceanique

Représentation de l’icosaèdre des plaques tectoniques majeures sur le globe

Le point d'intersection de deux bordures est un point de jonction de trois plaques. On peut repérer plusieurs de ces points triples sur la carte des plaques. En 1976, le Dr Athelstan Spilhaus (géophysicien et océanographe d'Afrique du Sud, consultant de National Oceanographic and Atmospheric Administration) examina ces points triples, en s'appuyant sur les résultats des recherches de Hanshou Liu au Goddard Space Flight Center, important centre de recherches de la NASA aux États-Unis. En les reportant sur un globe, il remarqua que les points triples coïncident presque parfaitement avec les sommets d'un icosaèdre.
Le Dr Spilhaus affirme que l'icosaèdre serait la dernière phase de l'évolution terrestre. En effet, la Pangée, au cours de sa dislocation, serait passée par trois phases. Elle aurait d'abord épousé la trame d'un tétraèdre, puis celle d'un cuboctaèdre (un cube tronqué à ses sommets), et enfin celle actuelle de l'icosaèdre associé au dodécaèdre.
Si les plaques avaient dérivé de façon chaotique, cette succession de géométries régulières serait bien surprenante. Mais si on admet que la Terre est structurée par une armature constituée des polyèdres de Platon, on peut comprendre que cette armature est le siège de concentrations de forces qui peuvent induire les fissurations ou guider les déplacements des masses.

Le 12 mars 2023 à 09:39:10 :
Bonjour.
Ne vous renseignez pas sur tout cela. Cela ne vous mènera qu'à votre propre perte. Toutes les "connaissances" ne sotn pas bonnes.

Salut l'ami.
Je dirais plutôt ne vous renseignez pas TOUS sur TOUT. L'initiation se fait par pallier. Mais vu la longueur de mes textes je pense que le tri est vite fait !