Help jsuis en controle de maths

Le 06 janvier 2025 à 15:54:23 :

Le 06 janvier 2025 à 15:54:07 :
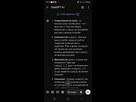
La reponse est 0

Preuve plz

1. Puisque sin(n) est borné et ne s'annule pas pour une infinité de n, n sin(n) diverge vers l'infini en valeur absolue.
2. Ainsi, 1/nsin(n) tend vers 0 lorsque n tend vers infini

Le 06 janvier 2025 à 16:04:44 :

Le 06 janvier 2025 à 15:54:23 :

Le 06 janvier 2025 à 15:54:07 :
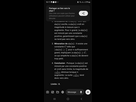
La reponse est 0

Preuve plz

1. Puisque sin(n) est borné et ne s'annule pas pour une infinité de n, n sin(n) diverge vers l'infini en valeur absolue.
2. Ainsi, 1/nsin(n) tend vers 0 lorsque n tend vers infini

Si je pose Un = 1/n alors Un est bornée et ne s'annule pas

Et 1/(nUn) tend vers 1

Tu peux disposax aussi

Le 06 janvier 2025 à 16:06:20 :

Le 06 janvier 2025 à 16:04:44 :

Le 06 janvier 2025 à 15:54:23 :

Le 06 janvier 2025 à 15:54:07 :
La reponse est 0

Preuve plz

1. Puisque sin(n) est borné et ne s'annule pas pour une infinité de n, n sin(n) diverge vers l'infini en valeur absolue.
2. Ainsi, 1/nsin(n) tend vers 0 lorsque n tend vers infini

Si je pose Un = 1/n alors Un est bornée et ne s'annule pas

Et 1/(nUn) tend vers 1

Tu peux disposax aussi

Cette situation est très différente de celle de la suite 1/nsin(n)

Sin(n) est bornée mais n'est pas egal à 1/n il oscille entre -1 et 1 sans tendre vers une valeur fixe

Le 06 janvier 2025 à 16:10:12 :

Le 06 janvier 2025 à 16:06:20 :

Le 06 janvier 2025 à 16:04:44 :

Le 06 janvier 2025 à 15:54:23 :

Le 06 janvier 2025 à 15:54:07 :
La reponse est 0

Preuve plz

1. Puisque sin(n) est borné et ne s'annule pas pour une infinité de n, n sin(n) diverge vers l'infini en valeur absolue.
2. Ainsi, 1/nsin(n) tend vers 0 lorsque n tend vers infini

Si je pose Un = 1/n alors Un est bornée et ne s'annule pas

Et 1/(nUn) tend vers 1

Tu peux disposax aussi

Cette situation est très différente de celle de la suite 1/nsin(n)

Sin(n) est bornée mais n'est pas egal à 1/n il oscille entre -1 et 1 sans tendre vers une valeur fixe

D'accord donc t'as rien prouvé à part dire c'est une situation différente
Bref tu ne fais pas de maths
Tu peux disposer

Le 06 janvier 2025 à 15:56:35 :

"ça devient très grand, ça devient très petit" sacré baratineur ce chatpgt

Le 06 janvier 2025 à 16:14:41 :

Le 06 janvier 2025 à 16:10:12 :

Le 06 janvier 2025 à 16:06:20 :

Le 06 janvier 2025 à 16:04:44 :

Le 06 janvier 2025 à 15:54:23 :

> Le 06 janvier 2025 à 15:54:07 :

>La reponse est 0

Preuve plz

1. Puisque sin(n) est borné et ne s'annule pas pour une infinité de n, n sin(n) diverge vers l'infini en valeur absolue.
2. Ainsi, 1/nsin(n) tend vers 0 lorsque n tend vers infini

Si je pose Un = 1/n alors Un est bornée et ne s'annule pas

Et 1/(nUn) tend vers 1

Tu peux disposax aussi

Cette situation est très différente de celle de la suite 1/nsin(n)

Sin(n) est bornée mais n'est pas egal à 1/n il oscille entre -1 et 1 sans tendre vers une valeur fixe

D'accord donc t'as rien prouvé à part dire c'est une situation différente
Bref tu ne fais pas de maths
Tu peux disposer