Topic de GhulAlRas :
(MATHS) limite INTROUVABLE
Données du topic
- Auteur
- GhulAlRas
- Date de création
- 16 juin 2024 à 22:12:32
- Nb. messages archivés
- 9
- Nb. messages JVC
- 9
En ligne sur JvArchive
JvArchive compagnon
Découvrez JvArchive compagnon , l'userscript combattant la censure abusive sur le 18-25 !




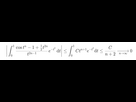

_.gif) (e -1)/(4e)
(e -1)/(4e) 


