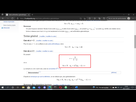
[Maths] Suites adjacentes

Le 04 novembre 2021 à 22:46:50 :
Je vois clé, mais comment trouver Un avec Un+1 ? Si je trouve ça le tour est joué
Ca marche pas par récurrence ?
Puisque t'as U_n+1 = f(U_n) ça devrait bien fonctionner je pense.
Le 04 novembre 2021 à 22:49:06 :
Le 04 novembre 2021 à 22:46:50 :
Je vois clé, mais comment trouver Un avec Un+1 ? Si je trouve ça le tour est jouéCa marche pas par récurrence ?
Puisque t'as U_n+1 = f(U_n) ça devrait bien fonctionner je pense.
Je vais essayer ça et je te dis 
Je devrai dire quoi maintenant ?



Deux suites réelles (an) et (bn) sont dites adjacentes si l'une des suites est croissante (au sens large), l'autre suite décroissante (au sens large) et si la différence des deux converge vers 0.
1) Prouve que l'une est croissante et l'autre decroissante ( tu as juste a calculer un+2-un+1 > 0
2) pour prouver que la limite tend vers 0, je te conseille de faire une nouvelle suite qui est égale a la différence des deux, ensuite perso je l'écrirai sans preuve ça m'as l'air évident mais tu peut faire une reccurence sinon
Le 04 novembre 2021 à 23:13:20 :
On obtient Un = - (0,75^n) +1 et Vn = (0,75^n) +1 donc Un - Vn = - (0,75^n) +1 - (0,75^n) -1 = - 2*(0,25^n) qui tend vers n quand n tend vers l'infini puisque 0,75<1
Désolé, j'ai pas trop compris ta démarche, mais je te remercie quand même. 
Le 04 novembre 2021 à 23:14:54 :
Deux suites réelles (an) et (bn) sont dites adjacentes si l'une des suites est croissante (au sens large), l'autre suite décroissante (au sens large) et si la différence des deux converge vers 0.1) Prouve que l'une est croissante et l'autre decroissante ( tu as juste a calculer un+2-un+1 > 0
2) pour prouver que la limite tend vers 0, je te conseille de faire une nouvelle suite qui est égale a la différence des deux, ensuite perso je l'écrirai sans preuve ça m'as l'air évident mais tu peut faire une reccurence sinon
Je vois merci. 
Le 04 novembre 2021 à 23:16:48 :
Edit : ça colle moyen avec tes suite, bref gl désolé vraiment la flemme

Le 04 novembre 2021 à 23:13:20 :
On obtient Un = - (0,75^n) +1 et Vn = (0,75^n) +1 donc Un - Vn = - (0,75^n) +1 - (0,75^n) -1 = - 2*(0,25^n) qui tend vers n quand n tend vers l'infini puisque 0,75<1
"tend vers n" petit lapsus je pense 
Le 04 novembre 2021 à 23:09:37 :
Bon j'ai essayé leur astuce, j'ai réussi à prouver que (Vn-Un) est géo. Wn = 2*(3/4)^n, donc Wn est décroissante.
Je devrai dire quoi maintenant ?
Il faut bien dire que Vn-Un (que t'as appelée Wn) tend vers 0 quand n tend vers l'infini. La décroissance ne suffit pas. Par exemple la suite 0,5^n + 1 est décroissante mais elle ne tend pas vers 0 en l'infini...
Maintenant il faut que tu montres que l'une est décroissante et l'autre croissante. (soit Vn croissante et Un décroissante soit le contraire)
Pour montrer qu'une suite est croissante il suffit de montrer que Un+1-Un>0
Le 04 novembre 2021 à 23:20:48 :
Le 04 novembre 2021 à 23:13:20 :
On obtient Un = - (0,75^n) +1 et Vn = (0,75^n) +1 donc Un - Vn = - (0,75^n) +1 - (0,75^n) -1 = - 2*(0,25^n) qui tend vers n quand n tend vers l'infini puisque 0,75<1"tend vers n" petit lapsus je pense
oi je voulais dire tend vers 0 désolé
Le 04 novembre 2021 à 23:21:46 :
Le 04 novembre 2021 à 23:09:37 :
Bon j'ai essayé leur astuce, j'ai réussi à prouver que (Vn-Un) est géo. Wn = 2*(3/4)^n, donc Wn est décroissante.
Je devrai dire quoi maintenant ?Il faut bien dire que Vn-Un (que t'as appelée Wn) tend vers 0 quand n tend vers l'infini. La décroissance ne suffit pas. Par exemple la suite 0,5^n + 1 est décroissante mais elle ne tend pas vers 0 en l'infini...
Maintenant il faut que tu montres que l'une est décroissante et l'autre croissante. (soit Vn croissante et Un décroissante soit le contraire)
Pour montrer qu'une suite est croissante il suffit de montrer que Un+1-Un>0
Tel que Un = - (0,75^n) +1 et Vn = = (0,75^n) +1 ? ( c'est ce que t'as trouvé, mais j'ai pas compris comment)

Le 04 novembre 2021 à 23:23:32 :
Le 04 novembre 2021 à 23:21:46 :
Le 04 novembre 2021 à 23:09:37 :
Bon j'ai essayé leur astuce, j'ai réussi à prouver que (Vn-Un) est géo. Wn = 2*(3/4)^n, donc Wn est décroissante.
Je devrai dire quoi maintenant ?Il faut bien dire que Vn-Un (que t'as appelée Wn) tend vers 0 quand n tend vers l'infini. La décroissance ne suffit pas. Par exemple la suite 0,5^n + 1 est décroissante mais elle ne tend pas vers 0 en l'infini...
Maintenant il faut que tu montres que l'une est décroissante et l'autre croissante. (soit Vn croissante et Un décroissante soit le contraire)
Pour montrer qu'une suite est croissante il suffit de montrer que Un+1-Un>0Tel que Un = - (0,75^n) +1 et Vn = = (0,75^n) +1 ? ( c'est ce que t'as trouvé, mais j'ai pas compris comment)
c'est simplement une formule à appliquer, plus haut j'ai fait une capture d'écran de la page wiki s'y rapportant. Mais tu avais déjà trouvé Un=f(n) et Vn=f(n) par toi-même non? 
Données du topic
- Auteur
- OkLM55
- Date de création
- 4 novembre 2021 à 22:42:18
- Nb. messages archivés
- 44
- Nb. messages JVC
- 44