[MATHS] Pensez-vous qu'à nous tous nous puissions résoudre la conjecture de Syracuse ?
Le 22 avril 2020 à 15:22:56 Doujinologue a écrit :
Le 22 avril 2020 à 15:20:42 Cornettotrilogy a écrit :
Doujinologue je pense que ta "preuve" ne prouve rien. Un peu de rigueur et de clarté ne ferait pas de malje suis actuellement en train de parler avec un matheux de ma preuve, je demande des conseils sur la rédaction car je sais que c'est catastrophique

je finis mes saisons d'animes et je me remets au travail sérieusement
Je pense que nous n'en verrons pas la finalité malheureusement 
Le 07 mai 2020 à 09:56:34 Yang_Mill a écrit :
Le 22 avril 2020 à 15:22:56 Doujinologue a écrit :
Le 22 avril 2020 à 15:20:42 Cornettotrilogy a écrit :
Doujinologue je pense que ta "preuve" ne prouve rien. Un peu de rigueur et de clarté ne ferait pas de malje suis actuellement en train de parler avec un matheux de ma preuve, je demande des conseils sur la rédaction car je sais que c'est catastrophique

je finis mes saisons d'animes et je me remets au travail sérieusement
Je pense que nous n'en verrons pas la finalité malheureusement

Je suis toujours là hein
Je me remets au niveau mathématique pour apprendre à rédiger correctement
Actuellement j'étudie les dérivées primitives, je vais passer aux suites après
Je vais trivialiser ça en 2-2, sans rigoler.
Le 08 mai 2020 à 20:44:24 Doujinologue a écrit :
Je suis toujours là hein
Je me remets au niveau mathématique pour apprendre à rédiger correctementActuellement j'étudie les dérivées primitives, je vais passer aux suites après
Je vais trivialiser ça en 2-2, sans rigoler.
Risible.
Le 08 mai 2020 à 20:44:24 Doujinologue a écrit :
Je suis toujours là hein
Je me remets au niveau mathématique pour apprendre à rédiger correctementActuellement j'étudie les dérivées primitives, je vais passer aux suites après
Je vais trivialiser ça en 2-2, sans rigoler.
Je viens de tomber sur ce topic. L'idée d'une collaboration publique autour d'un problème ouvert n'est pas en soi absurde ni même nouvelle (voir par exemple Polymath) et je pense même que pour apporter du "sang neuf" sur certains sujets la collaboration de matheux amateurs est la bienvenue.
Il y a "forcément" des idées intéressantes qui vont sortir. Je n'insiste même pas sur le fait de connaître des maths "sérieuses" parce que parfois la connaissance peut être un voile justement, qui empêche même d'imaginer de nouvelles choses.
Par contre à mon avis ça doit toujours se faire dans l'humilité et le respect, en particulier envers la communauté mathématique.
Malheureusement un certain nombre d'amateurs sont convaincus d'avoir démontré une conjecture difficile et tombent parfois dans des gros travers d'égo ou de communication. Du coup les vraies bonnes idées peuvent être noyées dans ce bruit.
Je ne sais pas trop comment résoudre ce souci...
Après, pour la conjecture de Syracuse, il y a eu du progrès récemment (voir les travaux de T. Tao notamment) donc je ne sais pas trop ce qu'une telle initiative donnera, surtout que ça n'est pas forcément le genre de projet qui se prête simplement à une collaboration de masse.
Le 24 juin 2020 à 04:21:00 wanadoo6 a écrit :
Je viens de tomber sur ce topic. L'idée d'une collaboration publique autour d'un problème ouvert n'est pas en soi absurde ni même nouvelle (voir par exemple Polymath) et je pense même que pour apporter du "sang neuf" sur certains sujets la collaboration de matheux amateurs est la bienvenue.Il y a "forcément" des idées intéressantes qui vont sortir. Je n'insiste même pas sur le fait de connaître des maths "sérieuses" parce que parfois la connaissance peut être un voile justement, qui empêche même d'imaginer de nouvelles choses.
Par contre à mon avis ça doit toujours se faire dans l'humilité et le respect, en particulier envers la communauté mathématique.
Malheureusement un certain nombre d'amateurs sont convaincus d'avoir démontré une conjecture difficile et tombent parfois dans des gros travers d'égo ou de communication. Du coup les vraies bonnes idées peuvent être noyées dans ce bruit.
Je ne sais pas trop comment résoudre ce souci...
Après, pour la conjecture de Syracuse, il y a eu du progrès récemment (voir les travaux de T. Tao notamment) donc je ne sais pas trop ce qu'une telle initiative donnera, surtout que ça n'est pas forcément le genre de projet qui se prête simplement à une collaboration de masse.
On l'a résolu hein c'est juste qu'on a gardé le résultat pour nous 
Le 24 juin 2020 à 04:21:00 wanadoo6 a écrit :
Je viens de tomber sur ce topic. L'idée d'une collaboration publique autour d'un problème ouvert n'est pas en soi absurde ni même nouvelle (voir par exemple Polymath) et je pense même que pour apporter du "sang neuf" sur certains sujets la collaboration de matheux amateurs est la bienvenue.Il y a "forcément" des idées intéressantes qui vont sortir. Je n'insiste même pas sur le fait de connaître des maths "sérieuses" parce que parfois la connaissance peut être un voile justement, qui empêche même d'imaginer de nouvelles choses.
Par contre à mon avis ça doit toujours se faire dans l'humilité et le respect, en particulier envers la communauté mathématique.
Malheureusement un certain nombre d'amateurs sont convaincus d'avoir démontré une conjecture difficile et tombent parfois dans des gros travers d'égo ou de communication. Du coup les vraies bonnes idées peuvent être noyées dans ce bruit.
Je ne sais pas trop comment résoudre ce souci...
Après, pour la conjecture de Syracuse, il y a eu du progrès récemment (voir les travaux de T. Tao notamment) donc je ne sais pas trop ce qu'une telle initiative donnera, surtout que ça n'est pas forcément le genre de projet qui se prête simplement à une collaboration de masse.
C'est une bonne idée, mais quand tu sais que Terence Tao s'y est penché et n'a pas réussi (du moins pour l'instant), ça démotive un peu.
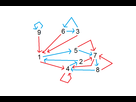
On définit l'application Syr de N\ {0} dans lui-même. Et on étudie l'orbite d'un entier N.
Le 15 avril 2020 à 18:15:52 Doujinologue a écrit :
Tout d'abord j'étudie la suite dans la définition [0;+inf[ sans le zéroOn sait qu'un nombre pair est divisé par 2 et qu'un nombre impair multiplié par 3 et +1
Je simplifie la suite de la manière suivante : nous ne travaillerons qu'avec la somme digitale de chaque nombre et résultat
On dresse le tableau suivant en fonction de la parité du nombre départ et de sa somme digitale
Le nombre digital parent est en gras et le nombre digital enfant est souligné1/2 = 0,5
5
1*3+1 = 42/2 = 1
2*3+1 = 73/2 = 1,5
6
3*3+1 = 101
4/2 = 2
4*3+1 = 134
5/2 = 2,5
7
5*3+1 = 167
6/2 = 3
6*3+1 = 1910
1
7/2 = 3,5
8
7*3+1 = 224
8/2 = 4
8*3+1 = 257
9/2 = 4,5
9
9*3+1 = 2810
1
On peut dresser l'a figure suivante où grâce à ça
- Les chiffres représentent la somme digitale du nombre X
- Les flèches désignent quelle opération l'ont fait du nombre X (Flèche bleu/2) ( Flèche rouge
*3+1)
Ainsi nous voyons que peu importe le nombre de départ on peut atteindre chaque étape et donc tous les nombres sont liés entre eux mais on voit 3 exceptions :
Propiété 1 : Si on ne commence pas par un nombre dont la somme digitale est de 3 6 ou 9 il sera impossible d'en avoir (représenté par les flèches à sens unique)
Proprité 2: On sait aussi que si le nombre X est impair alors le prochain calcul donnera forcément un nombre pair donc flèche rouge
Avec la Propriété2 il ne peut donc pas avoir 2 opérations impairs à la suite
Donc le nombre X aura qu'un nombre égal d'étapes et devra alterner pair et impair pour boucler, car s'il y a que des opérations pairs ou plus d'opérations pair qu'impaire, il tendra vers 1 donc la boucle 4 2 1
Il faut trouver des boucles qui boucles comme : IP , IPIP, IPIPIP etc..
Comme les 9I 6I 3I sont à sens uniques et bouclent sur du pair elles vont tendre vers 1
On doit qu'utiliser les 1I 2I 4I 5I 7I 8I 1P 2P 4P 5P 7P 8P car elle
dans une suite de + de 2 nombres ne doit pas contenir un 7P car il donnera un 8I et bouclera sur 7P8I etc
Etant la seule boucle qui alterne Pair et Impair avec 2 éléments on doit passer à des boucles de 3 éléments ou + et donc exclure 7P et 8I
Boucles possibles : 7P8I
---
Le seul moyen d'accèder à 5 est par un 1P, donc 5P n'est pas disponible
Possibilités restantes : 1I 2I 4I 5I 7I 1P 2P 4P 8P
Donc 5I mènera forcément à 7P, or ce n'est pas une boucle valable donc on supprime 5I
Si on supprime 5I et 5P il faut supprimer 1P qui était le seul chemin qui y menaitPossibilités restantes : 1I 2I 4I 7I 2P 4P 8P
Pour avoir un 8P il faut un 7P or ce n'est pas possible 2P à la suite
Possibilités restantes : 1I 2I 4I 7I 2P 4P
La suite 2I 7I n'est pas possible
Possibilités restantes : 1I 4I 2P 4P
4I ne peut pas boucler sur lui même car seul chemin venant vers 4 et 1I
Possibilités restantes : 1I 2P 4P
Nous avons donc que 2 boucles possibles
1 à 2 éléments : 7P 8I
1 à 3 éléments : 1I 2P 4POr selon forumeur vinsmock il est impossible d'alterner infiniment entre pair et impair
Comme une boucle pair impair est impossible le nombre diminuera forcément et donc tendra vers 4P 2P 1I
il y a un truc qui va pas tout au long de la preuve : tu supposes qu'un nombre pair divisé par 2 est forcément impair
.gif)
En revanche gg à lui d'avoir le courage de se lancer dans ce type de problème réputé impossible.
Aya Aberkane qui vient concurrencer ce topic http://idrissaberkane.org/wp-content/uploads/2020/07/Syracuse_2020-1.pdf
https://twitter.com/idrissaberkane/status/1007509389065023489
.gif)
Données du topic
- Auteur
- Otheocir
- Date de création
- 14 avril 2020 à 23:59:03
- Nb. messages archivés
- 1507
- Nb. messages JVC
- 1507